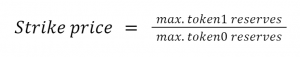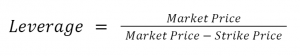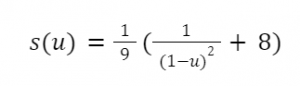Overview

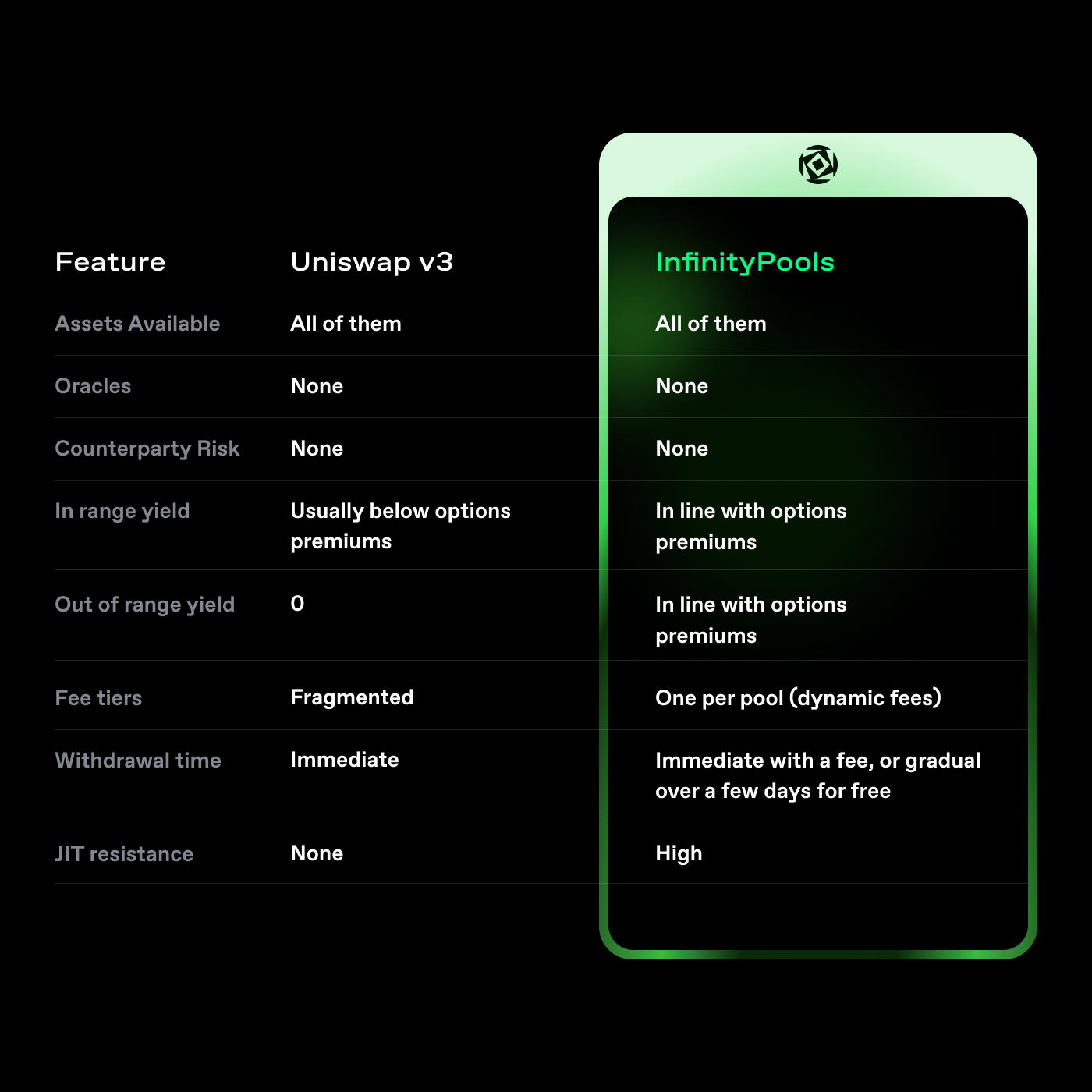
Infinity Pools is a decentralized exchange that can offer trading for any asset with unlimited leverage, no counterparty risk, no risk of liquidation, and no oracles.

Infinity Pools aims to disrupt the traditional perpetual futures trading models in DeFi by introducing a groundbreaking approach. It addresses the limitations of order book models and AMMs by enabling the trading of long-tail assets with leverage, without relying on oracles. 

• Permissionless listing and trading of any asset with existing liquidity and without bureaucratic constraints. 
• Traders can access significantly higher leverage, ranging from 1,000x to 5,000x on crypto assets, 10,000x to 20,000x on forex pairs, and up to 100,000x on correlated or pegged assets like stablecoins.
• No liquidation penalties, ensuring that more capital remains between traders and market makers, improving expected returns.
• No counterparty risk. Infinity Pools doesn’t rely on oracles, and positions are settled in a predetermined, mathematically guaranteed manner.

Practical Example

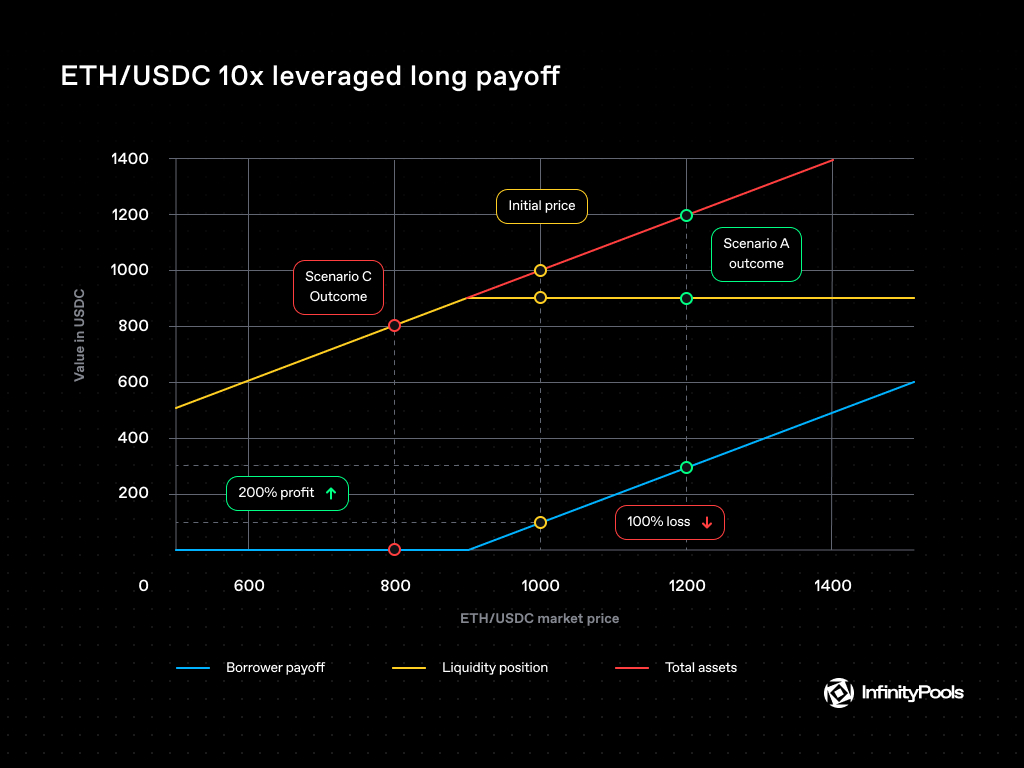
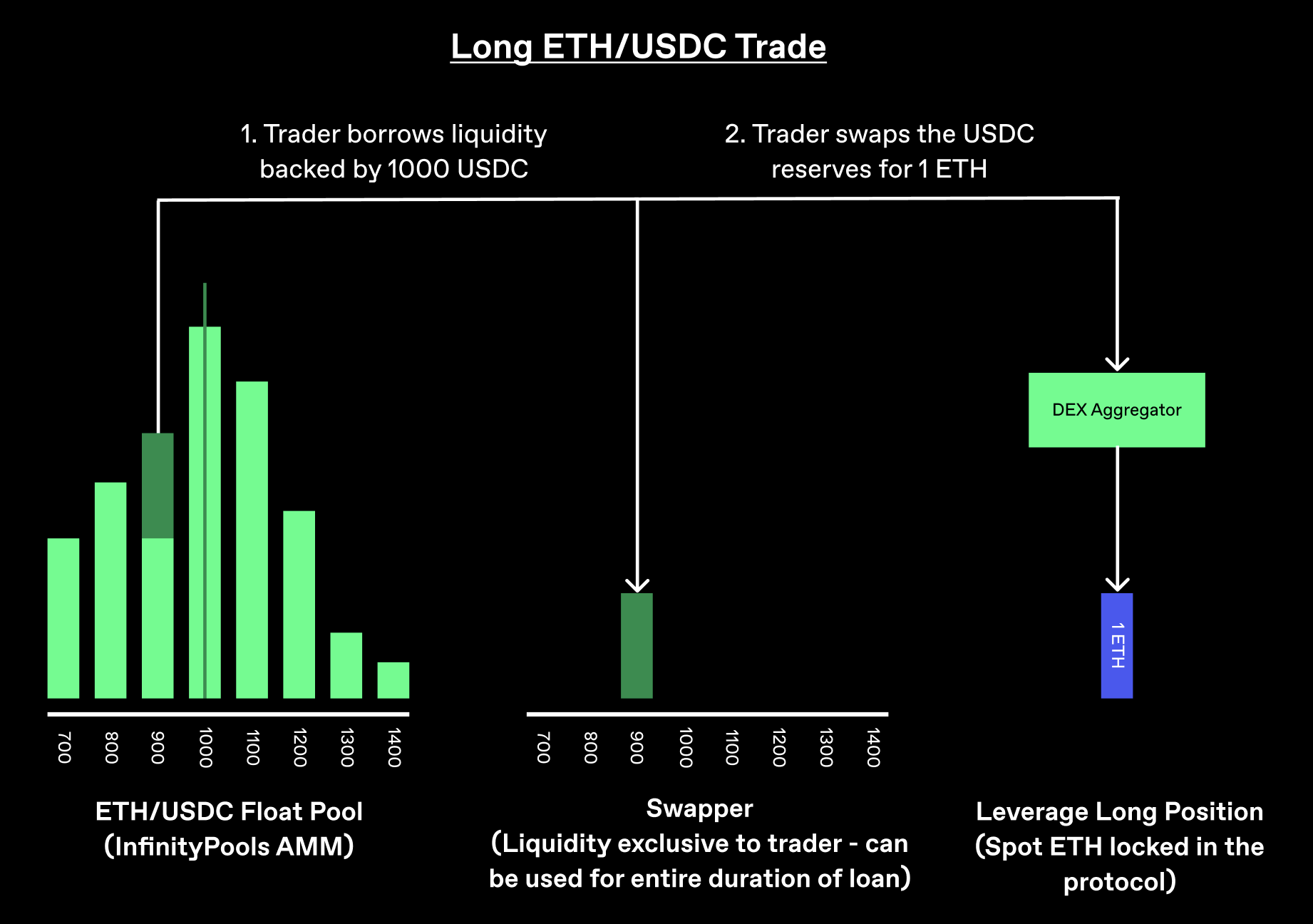
Let’s delve into a practical scenario illustrating the process of leveraged trading on InfinityPools using an ETH/USDC liquidity pair as an example:

1. A liquidity provider lends out an ETH/USDC LP token worth 1000 $USDC, positioned within a tight liquidity range centered at 900 $USDC.
2. A trader seeks to go long on $ETH with leverage. They borrow the ETH/USDC LP token and redeem it for 1000 $USDC.
3. Assuming the current $ETH market price is 1000 USDC, the trader swaps 1000 USDC for 1 ETH (adjusted for fees and slippage) using a spot DEX of their choice.

This can result in one of the following potential outcomes:

• A. $ETH price increases: If the price of $ETH rises, the trader profits. They can swap a portion of the 1 $ETH for 1000 $USDC to repay the LP token.
• B. $ETH price drops slightly: If the $ETH price falls just above 900 $USDC, the trader holds 1 $ETH (worth 900 $USDC), but the LP token is valued at 1000 $USDC. To fully repay the LP token, the trader needs to keep 100 $USDC (~0.11 $ETH) in collateral.
• C. $ETH price drops below 900 $USDC: If the $ETH price drops below 900 $USDC, the LP token’s value is equivalent to 1.11 $ETH. Since the trader already holds 1 $ETH (worth ~900 $USDC), they need 100 $USDC or 0.11 ETH in collateral to repay the full LP token.

We can observe that the minimum collateral required for borrowing a 1000 $USDC LP token at a 900 $USDC liquidity range is approximately 100 $USDC (~10x leverage). The closer the borrowed liquidity range aligns with the current ETH price, the higher the potential leverage. For instance, if the liquidity range is positioned at 999 $USDC, the required initial collateral is just 1 $USDC, yielding 1000x leverage.

The Trade Payoff Function

The trade payoff functions for the trader and liquidity providers are depicted in a chart. The chart doesn’t consider interest rates paid. Assuming normal volatility levels, the borrower’s interest payment for a one-day trade could be around 1 $USDC (~0.1% daily rate).

As the ETH price drops below 900 $USDC, the trader’s position remains open, and the same payoff function continues to apply unless the loan is closed out.

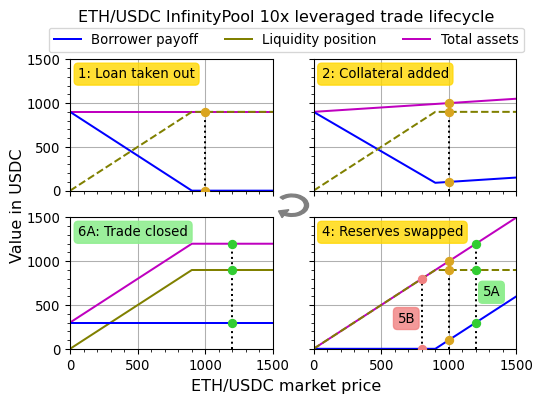
Full Trade Lifecycle

InfinityPools’ unique design ensures that the trade payoff aligns with a vanilla option, eliminating the concept of liquidation. 

The borrower’s payoff begins as an OTM (out-of-the-money) put option. Swapping reserves transforms the payoff into that of an ITM (in-the-money) call option.

This flexibility to switch between in-the-money and out-of-the-money positions allows traders to lock in profits or realize the position’s value in $USDC at any point before loan maturity. By converting a deep ITM call into a deep OTM put plus cash, the position’s value shifts primarily to cash, making it possible for traders to efficiently manage and capitalize on their leveraged positions.

The charts below are meant to be read in a clockwise fashion.

Options Analogy

The mechanism of InfinityPools can be explained using traditional finance instruments such as options and margin trading.

Trading

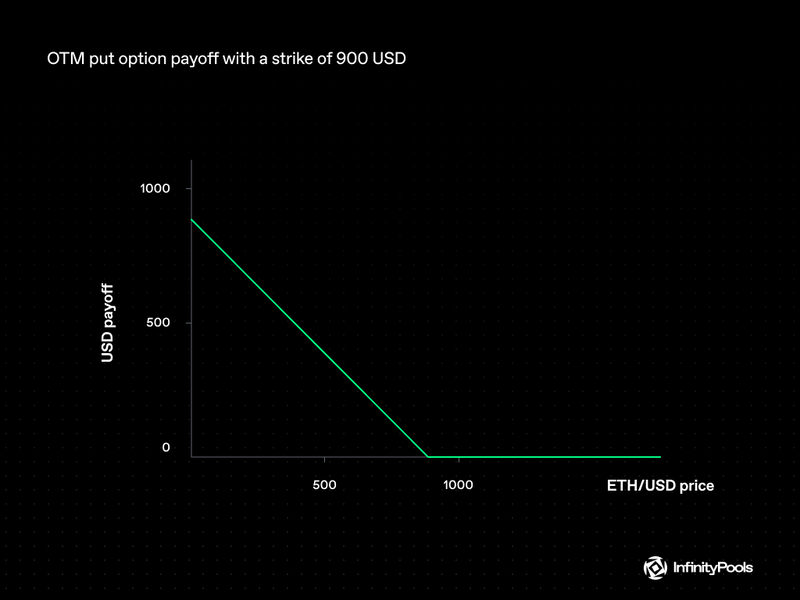
Traders on InfinityPools engage in what feels like margin trading, but the underlying mechanics resemble a synthetic ITM option. This is constructed by starting a margin trade and simultaneously purchasing an OTM option at a strike price that would typically represent the liquidation point in conventional margin trading. This creates a dual mechanism where the OTM option’s notional and expiry match the margin trade’s parameters, crafting a synthetic payoff similar to an ITM call option without the risk of liquidation.

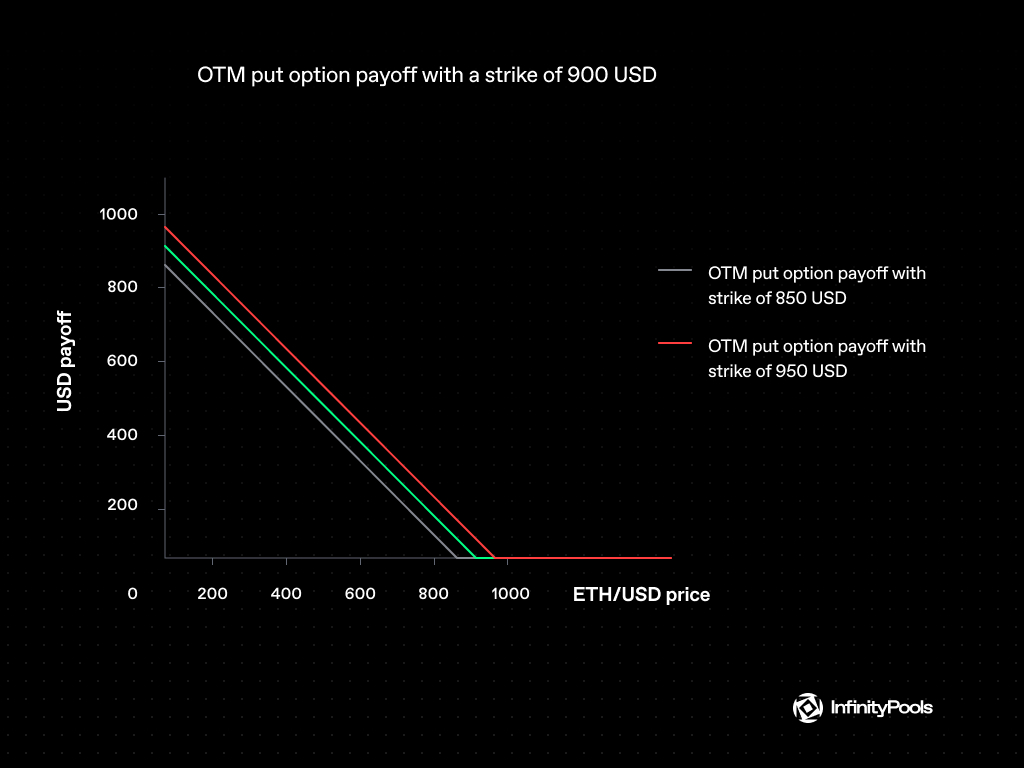
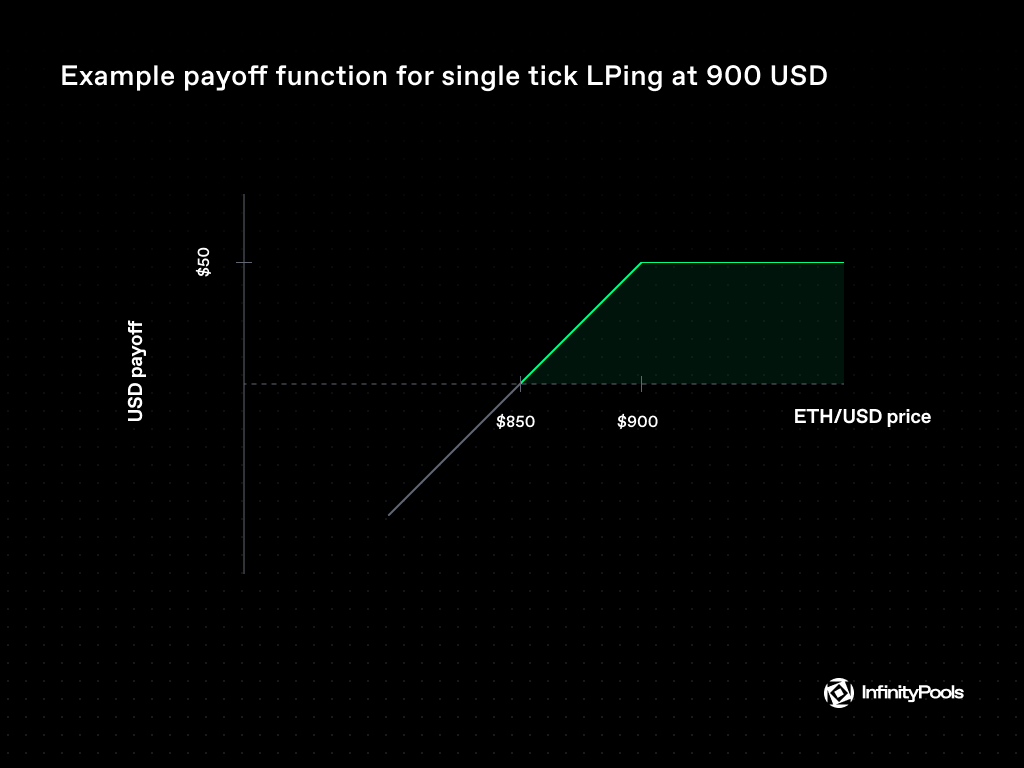
For instance, a trader looking to long ETH/USD with 10x leverage, with $ETH at 1000 USD, would buy an OTM put option with a strike of 900 USD.

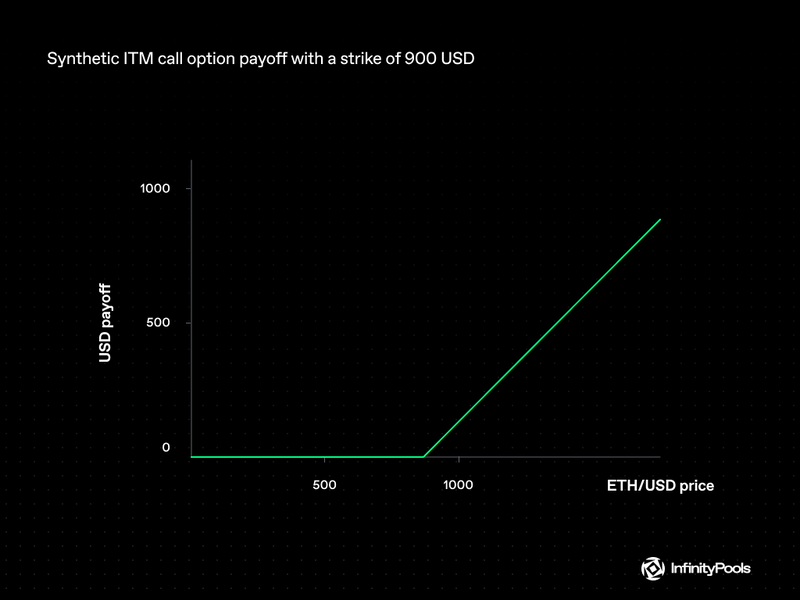
By swapping the borrowed USD for $ETH, the trader effectively creates a margin trade with a synthetic ITM call option payoff as seen below.

This structure allows traders to lock in profits or realize their position value in USD anytime before the maturity of the loan and option.

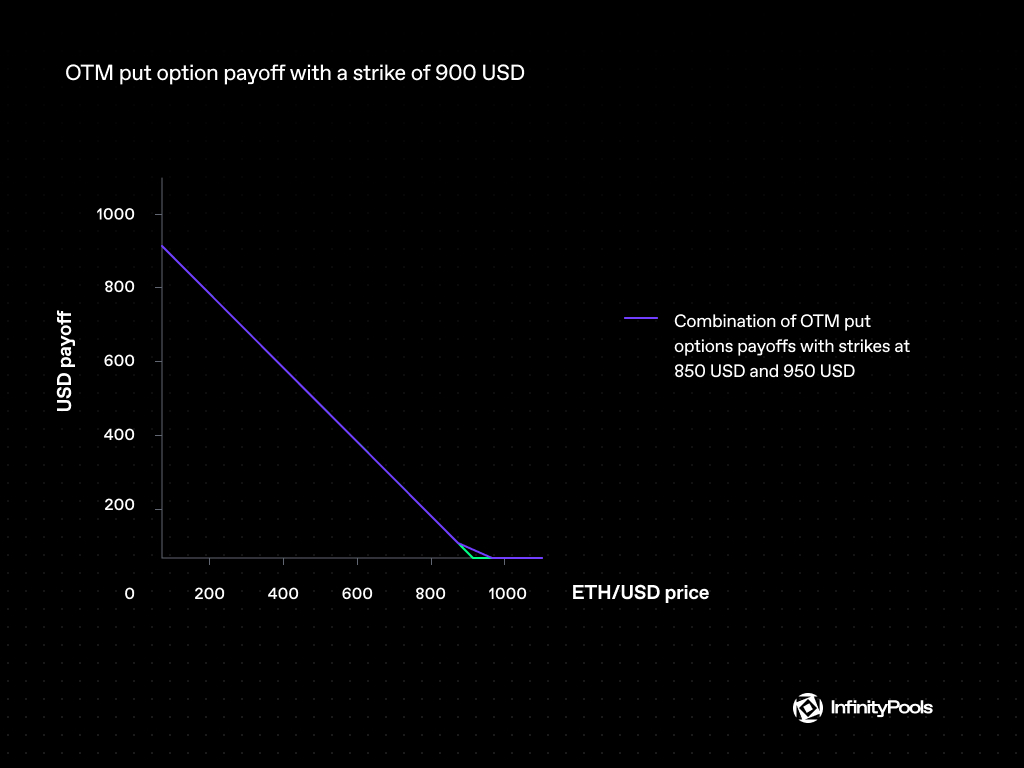
Furthermore, InfinityPools automatically mixes OTM options at various strikes (red and grey lines below) to produce the required payoff for the lowest possible premium if it lacks sufficient liquidity for an OTM option at the specified strike (green line below).

Because it has a strictly higher payoff than the original OTM option (green line below), this new synthetic OTM option (purple line below) is likewise suitable for the trade mentioned above.

Maturity Profile

The maturity framework within InfitityPools regarding options and loans is characterized by an exponential maturity with a half-life of one day. This setup ensures that traders maintain continuous exposure to the ETH/USD pair, even as individual trades and options approach expiration.

Opting for an exponential maturity rather than a conventional one-day maturity offers several advantages:

• Unified Expiry Schedule: This setup ensures that all options, regardless of when they were initiated, expire on the same schedule. This uniformity eliminates fragmentation across different expiration times, streamlining the trading process.
• Mitigation of MEV Risks: Exponential maturity helps mitigate miner-extractable value (MEV) risks, such as front-running, which can occur when trades are predictably settled at specific times. By avoiding a fixed daily swap-over, InfinityPools protects traders from potential predatory trading strategies.
• Efficient Pricing: The platform’s mathematical models for pricing exponentially maturing trades have proven to be more accurate and computationally cheaper than traditional models like Black-Scholes, enhancing both performance and cost-effectiveness.

Additionally, InfinityPools offers three main types of loan instruments:

• Fixed Term Loan: Similar to a European synthetic option, this loan type does not allow for exercise before maturity. However, traders can still lock in profits at any point during the loan period, providing flexibility within a structured framework.
• Revolving Loan: This instrument closely resembles an American synthetic option but offers greater flexibility. Traders can receive refunds on unspent premiums if they decide to close their positions early. For example, if a trader pays a premium for an hour-long trade but exits after 30 minutes, they receive a 50% refund.
• Periodic Loan: Serving as the primary trading mechanism within InfinityPools, the periodic loan starts as a fixed-term loan and transitions to a revolving loan after a predetermined lock-in period. This hybrid structure combines the predictability of fixed-term loans with the adaptability of revolving loans.

These instruments, combined with the exponential maturity profile, allow InfinityPools to offer a trading environment that balances flexibility, efficiency, and security.

Market Making & Liquidity

LPs in InfinityPools act somewhat like market makers in traditional options markets but in a more automated and passive manner. They select asset pairs and price ranges to provide liquidity, selling covered options within these ranges. The unutilized assets are then employed as liquidity in the InfinityPools spot AMM.

Premium Calculation

In InfinityPools, LPs obtain their earnings from two primary sources: premiums from covered options and transaction fees from the spot trading activity within the InfinityPools AMM. 

The premium calculation for selling covered options in InfinityPools is a two-step process involving the following elements:

1. Minimum Premium Calculation: This is determined by a proprietary equation that resembles the well-known Black-Scholes model, commonly used for pricing options in traditional finance. InfinityPools’ adaptation of this model is tailored to more efficiently and accurately reflect the unique characteristics of blockchain-based assets and DeFi environments. The modifications likely address factors such as the continuous trading nature of cryptocurrencies, their volatility, and the decentralized aspect of the platform.
2. Utilization Rate: This component adjusts the premium based on the supply and demand for leverage. The utilization rate is a multiplier that enhances the base premium (minimum premium) in response to increased demand for leverage or when arbitrage opportunities arise. This mechanism ensures that premiums are market-responsive, providing a compensation that is commensurate with the risk undertaken by liquidity providers.

To contextualize the premium calculation, consider an example where the combined income from option premiums and transaction fees totals $50 over a specific period. If LPs have deployed assets at a price level of 900 USD, the calculation would integrate both the base premium derived from the modified Black-Scholes formula and the adjusted multiplier from the utilization rate. This total sum represents the LP’s direct financial compensation for their risk exposure and provision of liquidity as seen on the graph below.

Advantages of InfinityPools vs Option Markets

InfinityPools offers several enhancements over conventional options markets:

• Permissionless Market Listing: Any tradable asset can quickly have a market created for it on the platform.
• Higher Leverage: Due to the granular level at which options are sold (theoretically unlimited strikes), higher leverage multiples are possible closer to the market price.
• Reduced Liquidity Fragmentation: By using spot liquidity for options creation, liquidity is not split between markets. This structure, combined with options sold across a larger number of strikes, allows for a more precise recreation of desired payoffs.
  • Unified Maturity Profile: The exponential maturity profile of options in InfinityPools eliminates fragmentation across different expiries, aligning all options to expire on the same schedule and mitigating potential market manipulation.

An automated market maker is the central component of InfinityPools’ system. This makes it feasible to perform things that would be extremely difficult or impossible to achieve with standard options markets. 

Protocol Mechanisms

Swappers

One of the unique features of InfinityPools is the introduction of a fundamental primitive called “Swappers.” This mechanism makes it possible to offer limitless leverage and eliminate liquidation risk. Essentially, swappers enable borrowing of pool liquidity to facilitate exclusive token swaps at a predetermined price.

In InfinityPools, traders can borrow liquidity from the pool to create a Swapper, which allows them to swap borrowed tokens (e.g., $ETH) for the other token in the pool (e.g., $USDC) at a predetermined price known as the “strike price”. This process involves taking into account the liquidity range and the maximum reserves of both tokens. Essentially, a swapper is borrowing the ability to swap tokens within the specified range. 

At its core, a Swapper allows traders to borrow liquidity from the pool. Borrowing this liquidity gives traders the exclusive right to swap the borrowed tokens (e.g., $ETH) for the other token in the pool (e.g., $USDC) at a predetermined price. This predetermined price is crucial as it ensures there is no liquidation risk. More specifically, by eliminating liquidation risk, InfinityPools can offer unlimited amounts of leverage for any asset.

When a swapper is created by borrowing a liquidity range or sum of ranges, it is “minted” with reserves whose amounts vary according to a predefined curve. These reserves are such that they can recreate the original liquidity ranges that the swapper borrowed. Essentially, the swapper holds enough tokens to ensure that the original liquidity can be reconstituted.

What this means is that while a swapper is being used, it must always maintain enough reserves such that it can recreate the original liquidity ranges it borrowed. This is crucial because it ensures that the liquidity providers who lent out these ranges do not take on any risk. The reserves remain secured.

For illustration, think of the reserves as tokens that are backing the borrowed liquidity range. As the swapper is used, and as the price moves within the range, these reserves are adjusted according to a curve that guarantees that there are always enough tokens to recreate the borrowed liquidity range.

It’s essential to differentiate this type of swap from the typical swap at market price used for entering long positions. The market price swap can be executed through any decentralized exchange or aggregator.

Leverage can be generated using a combination of diverse liquidity ranges, whether they are narrow or wide, and they don’t need to be adjacent. These ranges’ liquidity is aggregated into a singular entity known as a “swapper.” The tokens backing these aggregated liquidity ranges are termed “reserves.”

Swapper Strike Price

Every Swapper has a single predetermined price, known as its “strike price,” at which an unlimited number of token swaps can be performed for free (i.e., without slippage or fees) using its underlying reserves. The swapper’s strike price is situated at the midpoint of the liquidity used to produce leverage:

Here, token0 and token1 are the two tokens in the pool, and max reserves are the reserves when the pool price is below or above all borrowed liquidity ranges.

Let’s take the example where token1 is $USDC, token0 is $ETH, and the liquidity range borrowed is at 2,200 $USDC. If the max reserves of $USDC when the pool price is above the liquidity range are 2,400, and the max reserves of $ETH when the pool price is below the liquidity range is 1.09, the strike price is calculated as 2,400/1.09 = approximately 2,201.83 $USDC.

This system is beneficial because it allows for more flexibility and functionality (like using leverage), without compromising the security or integrity of the liquidity that has been provided to the pool.

Also, it’s worth noting that a swapper is constrained in such a way that its reserves curve is always above or equal to the liquidity range curve it originated from. This is a property of convex curves, and it guarantees that the swapper always has enough reserves to recreate the original liquidity ranges.

Creating Leverage 

Leverage can be created from an arbitrary number of wide or narrow liquidity ranges. These ranges can be adjacent or not. When a range (or sum of ranges) is borrowed in one transaction, it is aggregated into the Swapper. The tokens (e.g., $ETH & $USDC) that back these liquidity ranges for a given Swapper are called its reserves.

Swapper Reserves

Swappers are created from one or multiple liquidity ranges. Each swapper is initially minted with a specific amount of reserves, determined by a predefined curve that adjusts as the pool price fluctuates within the liquidity range. This setup ensures that the swapper always contains the exact reserve amount necessary to mirror the originating liquidity ranges. Once a swapper is lent out, its reserves are strictly regulated to ensure they are always sufficient to recreate the original liquidity ranges from which they were derived. 

By design, lending out liquidity ranges via swappers does not introduce credit risk for LPs. Borrowers of the liquidity gain access to use it but do not control the underlying reserves. These reserves remain securely locked, ensuring that they can always fulfill the requirements to recreate the initial liquidity conditions. 

This structured approach to managing swapper reserves means that LPs can lend their liquidity with confidence, knowing that the system inherently protects against the potential mismanagement or misappropriation of the lent assets.

Float Pool

InfinityPools introduces a concept known as the “float pool,” a dynamic liquidity pool akin to conventional concentrated liquidity models (akin to Uniswap v3). This internal float pool serves as the origin of loaned liquidity and contributes to a seamless trading experience while redefining yield-generation liquidity providers.

For users engaging in spot swaps, the float pool mirrors the behavior of traditional liquidity pools. This means that users executing spot swaps can interact with the float pool as they would with a conventional liquidity pool. Notably, the float pool can achieve lower fee levels and simultaneously offer enhanced LP yields due to the infusion of yield and volume stemming from lending liquidity.

InfinityPools LPs get paid both traditional spot AMM fees plus the interest rate from the swapper. This is because the InfinityPools AMM (aka the float pool) is just a regular spot AMM which liquidity is borrowed from. As a result, yield accrues more directly to liquidity providers through the interest rate that the borrower pays to hold the liquidity. This interest rate compensates the liquidity providers for the capital they have lent out through the protocol. Since traders borrow an actual LP token, liquidity providers continue earning yield from interest payments even if their liquidity is out of range in the underlying AMM. 

	AMM Liquidity Range	Swapper
Who can use it to swap tokens?	Anyone	Only the borrower
At what price will tokens be swapped?	Pool price (+ slippage)	Strike price (no slippage)
Where does the LP yield come from?	Swap fees	Interest payments (no swap fee)

With Infinity Pools, traders and LPs will always get paid at least the realized volatility if not implied volatility due to an arbitrage opportunity that uses lending as a floor on yields. Traders can buy volatility by going both long and short at the same time, betting that the premium paid upfront will be smaller than the probability of the asset’s price moving in either direction. 

Furthermore, trading fees and lending rates are intrinsically linked because there’s always an arbitrage opportunity that uses lending as a floor on yields, creating a floor for yields for LPs. Most Uniswap pools are currently being compensated below realized volatility levels, which is not ideal. However, with Infinity Pools, there is no real ceiling to how much compensation LPs can receive depending on the utilization rate and demand for leverage in a pool.

Loan Maturity

In InfinityPools, loans of liquidity ranges (swappers) follow an exponential maturity model, allowing traders to strategically manage their positions over time. 

Exponential Maturity

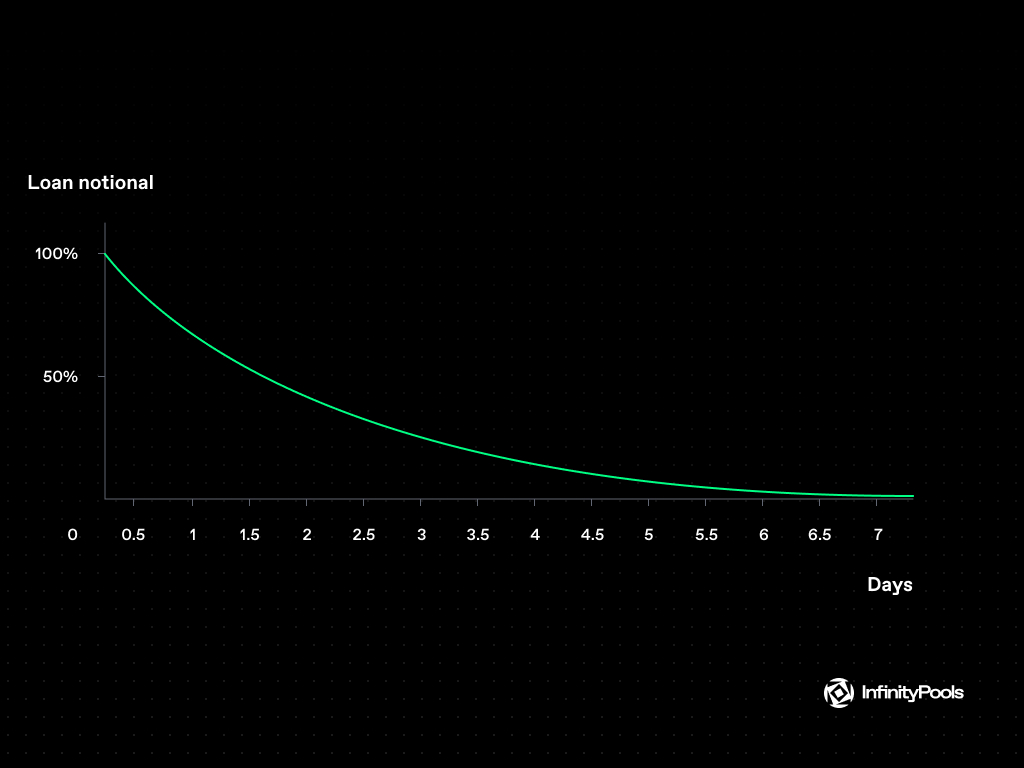
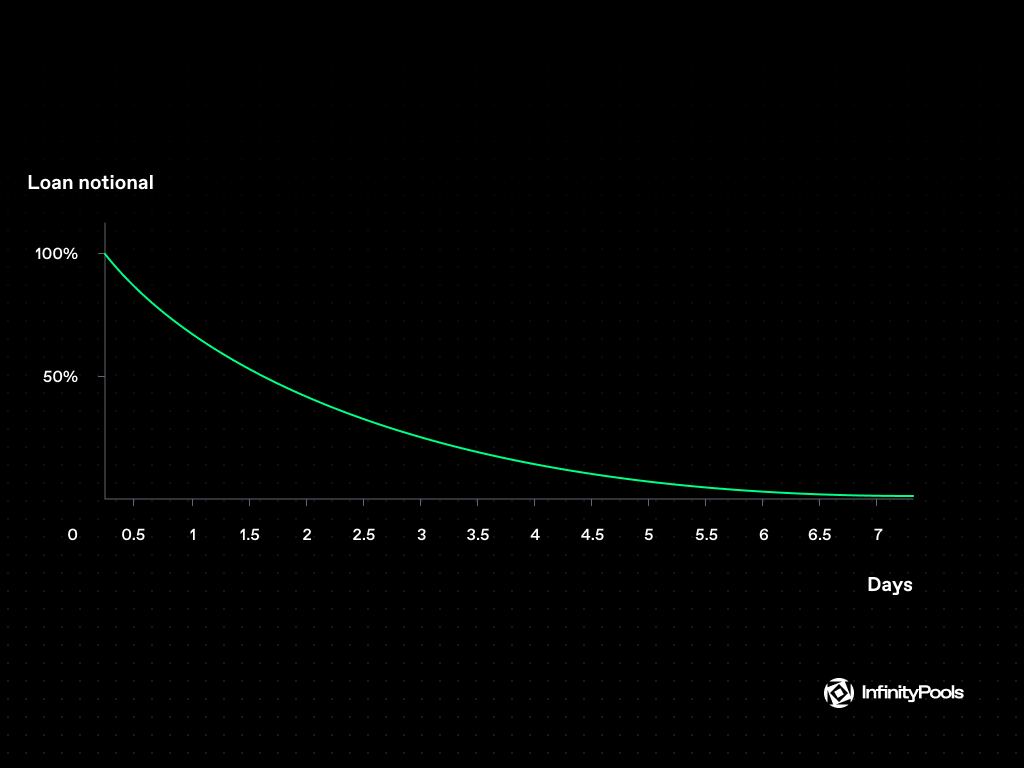
Loans of liquidity ranges on InfinityPools mature continuously, with the proportion of the position maturing remaining consistent at each instant. The amount of outstanding loans, therefore, follows an exponential decay function over time. For instance, if a trader borrows 1 $USDC, after some time t, the remaining $USDC on loan will be calculated using the exponential decay formula e^(-λt), where λ represents the decay constant.

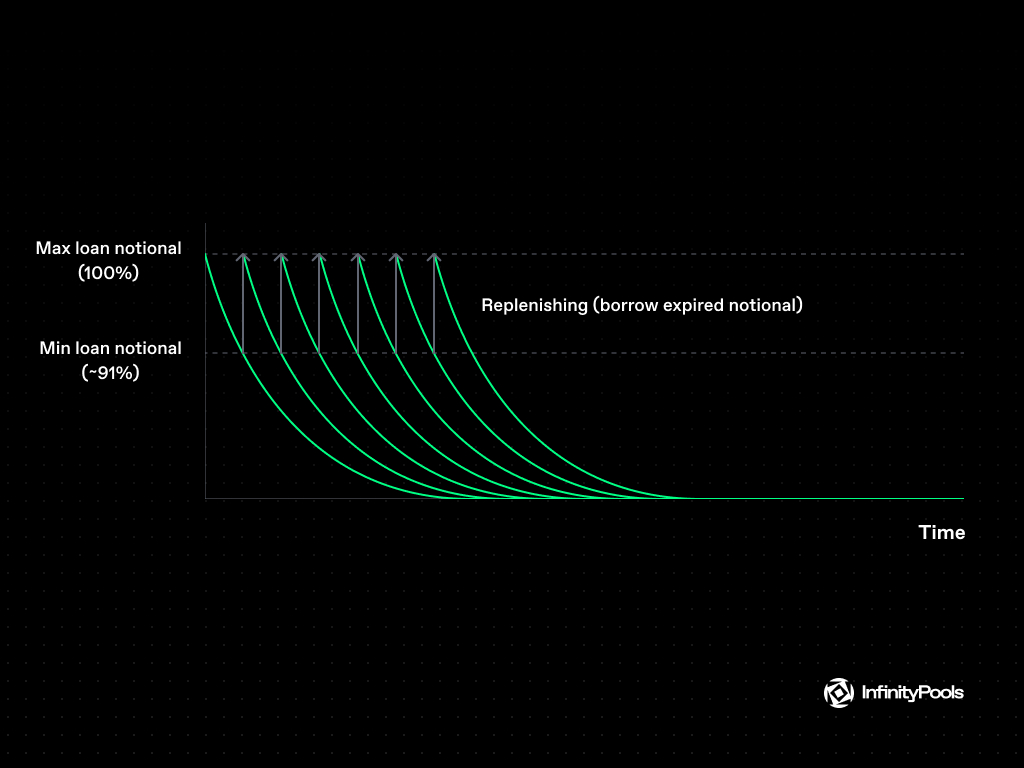
The image below shows the notional amount of a loan on Infinity Pools over 7 days.

Replenishing Process

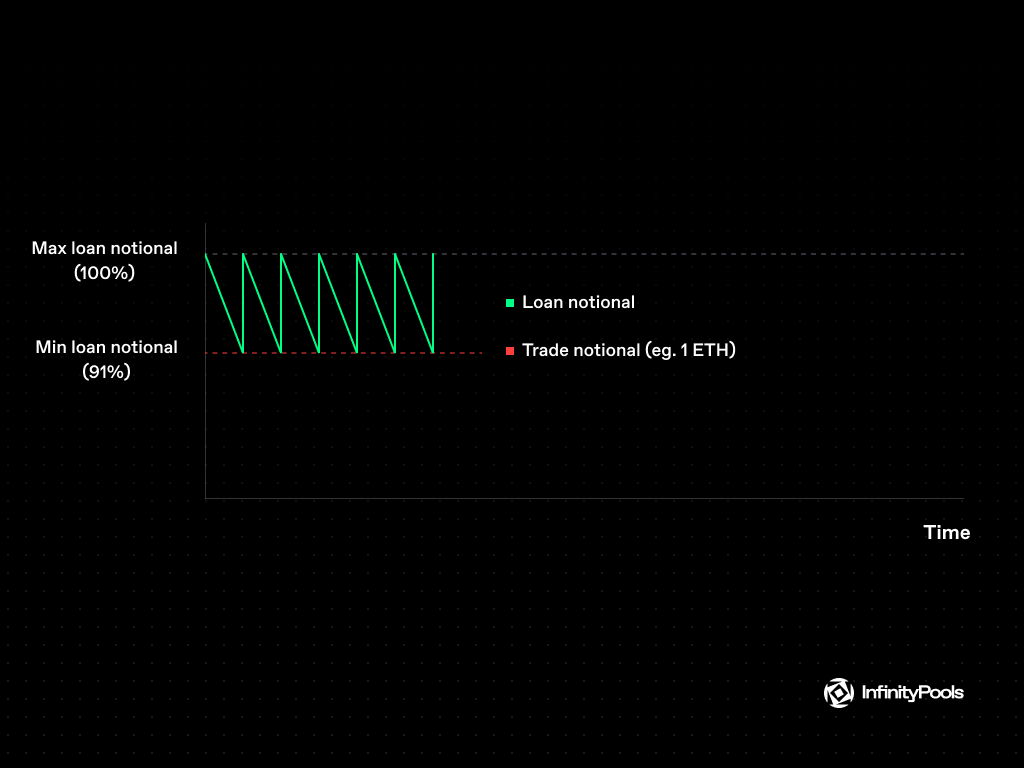
InfinityPools introduces a unique feature: the replenishing process. Traders have the option (but not the obligation) to replenish the portion of holdings that have decayed, at the prevailing interest rate. This strategic move ensures that traders’ position sizes remain constant over time, despite the natural decay of the loaned liquidity.

In practice, a trader who aims to go long 1 $ETH would borrow slightly more (e.g., 1100 $USDC) and then convert $1000 USDC into 1 $ETH. This proactive replenishing process guarantees that the trader’s exposure to $ETH remains unaltered, and it’s accomplished before the loan notional drops below the trade notional.

Estimated Time Left

The Estimated Time Left metric is shown on the user interface. It predicts how long a trader can maintain a leveraged position if the market price remains unchanged.

When traders enter positions using borrowed funds, they pay interest out of their margin. Over time, as they periodically renew their loans and pay new interest rates, the margin decreases. This cycle increases leverage since the same loan amount continues to demand more of the reducing margin.

The process continues until the margin can no longer cover the interest, leading to the cessation of loan renewals and the beginning of the position unwind. The Estimated Time Left measures the number of possible renewals before the margin runs out.

Market movements affect this timeline significantly. A price drop accelerates margin depletion and the unwinding process. Conversely, a price rise can use unrealized gains to extend the life of the position, allowing for more renewals. This metric helps traders gauge the durability of their positions and manage risks more effectively.

Parallels with Perpetual Futures

This replenishing mechanism in InfinityPools mirrors the concept of perpetual futures’ implicit settlement at the spot price. In perpetual futures, the forced replenishing of positions maintains a constant position size over time. This is achieved by having long position holders sell the asset at the spot price and then buy more futures at their mark price, thus offsetting the position’s decay due to funding rates.

However, this feature comes with limitations and complexities in the case of perpetual futures, leading to deviations between perpetual P&L and the spot market. InfinityPools’ approach circumvents these issues by making replenishing entirely optional and based on traders’ preferences.

Benefits of the Infinity Pools’ Approach

In Infinity Pools traders can set an interest rate tolerance that triggers replenishing when the APR exceeds their chosen threshold, ensuring position stability. 

For instance, if a borrower prefers not to pay more than 10% APR, they can set the threshold at 10%. When the APR surpasses 10%, the loan unwinds exponentially; conversely, when the APR drops below 10%, the notional grows back to its original level.

This optional replenishing model grants traders more control over their positions, eliminates dependency on excessive funding rates, and fosters a more stable and reliable trading experience.

Loan Types

Infinity Pools offers three types of loans:

• Fixed Term Loan: This loan offers leverage ranging from 1x to 40x. It is relatively cheaper and has a perpetual-like duration, where the loan is rolled forward every day. The interest on this loan is paid upfront.
• Revolving Loan: Offering much higher leverage, ranging from 40x to 2000x, this loan is more expensive compared to the fixed-term loan. However, it offers greater flexibility as it can be closed out at any time, and it does not require an upfront interest payment.
• Periodic Loan: A combination of the previous two. This loan starts as a fixed-term loan and becomes a revolving loan after a predetermined lock-in period.

In addition to collateral requirements, traders using InfinityPools must also consider the funds needed to pay interest on their loans. Fixed-term loans require upfront payment of interest, while ongoing loans that are rolled forward require continual replenishment of capital. If a trader fails to replenish the necessary funds, the position will be automatically wound down by the protocol.

To protect traders, InfinityPools allows them to set a maximum interest rate. If the interest rate exceeds this threshold, the protocol will unwind the loan and forgo rolling it forward. Conversely, when the interest rate falls back below the tolerance rate, the protocol will reactivate the position.

Fixed Term Loans

InfinityPools offers a fixed-term loan option that provides traders with controlled leverage at a more affordable cost. This type of loan is best suited for lower levels of leverage (approximately 1-40x) on high market capitalization assets.

Fixed-term loans have a predefined duration and are designed for traders seeking manageable leverage. Unlike other loan types, with fixed-term loans, the borrower needs to pay the interest due over the loan’s lifetime upfront. The protocol then disburses this interest to the liquidity range lenders according to predefined rules. 

While the loan has a set duration, traders have the flexibility to take profits from their trade by swapping the borrowed assets back to their original tokens at any point during the term.

The fair value interest rate for a fixed-term loan can be computed based on various parameters. Assuming the pool price follows a geometric Brownian motion with no drift, the formula to calculate the fair value interest rate is derived as follows:

One of the key advantages of fixed-term loans is their efficient implementation. Specific liquidity ranges used to create a loan do not need to be individually recorded. The repayment schedule is immutable and exponential, meaning that only the growth rate of liquidity available in each “tick” (bucket) needs to be tracked.

Interest for borrowing each liquidity range is paid upfront and collateralized, factored into the scheme in terms of liquidity range units. By knowing all the supplied and borrowed liquidity ranges, along with the interest paid, the protocol can determine the positions (available liquidity in each bucket of the float pool and the remaining notional for each fixed loan) for all future time points.

Revolving Loans

InfinityPools offers a second type of loan, known as a revolving loan, which caters to higher levels of leverage (approximately 40-1000x or more) on high market capitalization assets. This loan type introduces greater optionality for borrowers, making it a powerful tool for traders seeking dynamic leverage. 

Revolving loans are designed to provide traders with the flexibility to access higher levels of leverage, while also allowing for dynamic adjustments and early loan closure. Unlike fixed-term loans, revolving loans mature according to predefined rules, but they can be closed out by the borrower at any time. Closing out the loan effectively results in an immediate maturity, allowing the borrower to return the liquidity range to the pool. This makes the borrowed liquidity available again for lending or providing liquidity to the pool. When a revolving loan is closed, the borrower is no longer obligated to make further interest payments.

The key feature of revolving loans is their incremental interest payment structure. Borrowers do not need to pay interest upfront; instead, they have the option to post collateral incrementally to cover future interest payments. If a borrower closes out their loan before the term ends, they receive back any unspent collateral. This incremental interest payment mechanism enables borrowers to achieve higher ratios of the amount borrowed to the capital provided, resulting in higher leverage ratios.

Revolving loans require recording the liquidity ranges used to create each loan. This is essential to accurately determine the interest to be paid to each underlying bucket when the loan is closed and liquidity ranges need to be returned to the pool. This recording process ensures transparency and accuracy in interest calculations

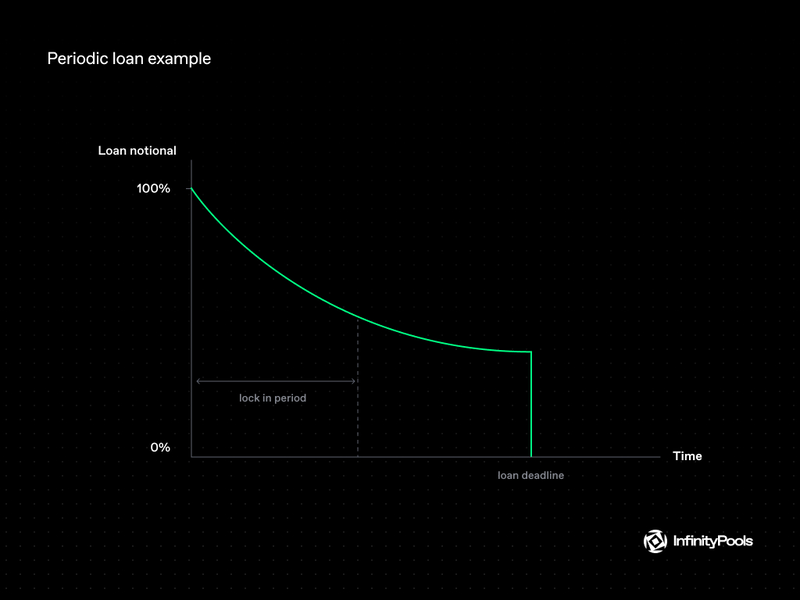
Periodic Loans

Periodic Loans are the main type used by InfinityPools, which merges characteristics of both fixed-term and revolving loans. This hybrid loan type begins its lifecycle as a fixed-term loan. After completing a predefined “lock-in” period, it transitions into a revolving loan, which allows for continuous borrowing and repayment within the established credit terms.

In the design of the Infinity Pools protocol, the flexibility of this loan type is emphasized by its adjustable lock-in period. Specifically, a periodic loan configured with a zero-day lock-in functions effectively as a revolving loan, offering ongoing access to funds without a set repayment schedule. Conversely, a periodic loan with an indefinitely long lock-in period operates as a fixed-term loan, with a clear start and end date but no flexibility for mid-term adjustments.

Utilization Rate and Effective Interest  Rate

In InfinityPools, the effective interest rate paid to lenders consists of two components: 

• Fair value interest rate.
• Utilization rate. 

This structure ensures that lenders receive competitive returns while borrowers can access liquidity at reasonable rates.

Fair Value Interest Rate as the Floor Rate

The fair value interest rate serves as the baseline for borrowing and lending assets on InfinityPools. It is determined based on various factors and represents the expected returns for both borrowing assets and providing liquidity in the float pool. Lenders would not want to lend their assets below the fair value rate, as their potential returns would be lower than what they could earn from the underlying float pool. Therefore, the fair value rate acts as the “floor rate” for borrowing assets.

Utilization Rate and Scaling Factor

The utilization rate is a key parameter that determines how the effective interest rate scales based on the demand for borrowing assets. For each liquidity bucket (or “tick”), the utilization ratio (the proportion of liquidity on loan compared to the total supply) is calculated. The scaling factor, denoted as s(u), is a function of this utilization ratio.

The formula for calculating the borrow rate for a given bucket is:

Borrow Rate = Scaling Factor s(u) x Floor Rate

Balancing Demand and the Effective Rate

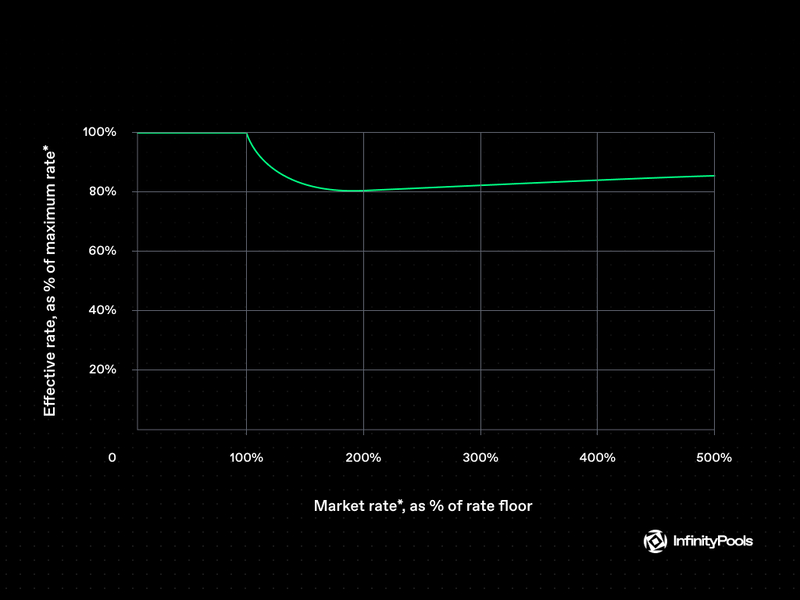
The utilization rate is designed to strike a balance between borrowers’ demand for assets and lenders’ returns. It ensures that the effective interest rate paid to lenders remains competitive while accommodating borrowers’ needs. The goal is to approximate the maximum market interest rate (r*) that borrowers are willing to accept, while also ensuring that the effective rate is stable relative to changes in the utilization ratio.

Effective Rate = (u x s(u) + 1 – u) x Floor Rate

The scaling factor s(u) is carefully chosen to achieve these objectives. It is designed to minimize the difference between the effective interest rate and the maximum achievable rate (r*) while ensuring stability as the utilization ratio changes. The specific scaling factor used is:

This scaling factor guarantees that liquidity providers earn an effective rate that is at least 84% of the maximum achievable rate (r*), regardless of the value of r*. It balances the interests of both borrowers and lenders, resulting in a system that provides competitive rates and stability across varying utilization ratios.

The image below shows how close the effective interest rate gets to the maximum interest rate r*, over a range of market rates r*. 

Rate Router

Infinity Pools incorporates an off-chain component known as the Rate Router to enhance the trading experience for users accessing the platform via the official website or API. This tool is essential in sourcing liquidity for trades in a “peer to pool” fashion, effectively addressing and mitigating issues of liquidity fragmentation.

The Rate Router is designed to ensure that traders receive the most favorable interest rates available for their trades while facilitating the replenishment of their positions. It achieves this through several innovative protocol features:

• Liquidity Ranges: The protocol allows for liquidity ranges that support extremely high leverage levels—up to 1000x. Importantly, these ranges are also applicable to all lower leverage tiers (from 1x to 999x), providing a broad spectrum of trading options within a single framework.
• Combination of Liquidity Ranges: Traders have the flexibility to combine different liquidity ranges to achieve their desired leverage multiple. For example, if a trader aims to go 10x long on ETH priced at 1000 USDC, they can choose to borrow liquidity centered around 900 USDC or mix liquidity centered at 850 USDC and 950 USDC in appropriate proportions to optimize their position.

The Rate Router simplifies the process of managing these complexities. When a trader specifies a leverage multiple, the router automatically searches for and combines the best liquidity ranges, ensuring optimal interest rates without the trader having to manually intervene. This functionality can be likened to how Uniswap’s price router operates but is specifically tailored for managing InfinityPools’ interest rates.

Matching Engine

InfinityPools introduces an off-chain component known as the matching engine, designed to enhance the trading and liquidity provision experience by eliminating liquidity fragmentation and optimizing interest rates. This matching engine facilitates efficient “peer to pool” interactions between traders and liquidity providers.

• One of the key features of InfinityPools is its utilization of liquidity ranges, which enables higher levels of leverage (such as 1000x) as well as all levels of leverage below it (ranging from 1x to 999x). This flexibility empowers traders to tailor their leverage according to their preferences and risk tolerance.
• Traders can combine separate liquidity ranges to achieve a desired leverage multiple. For instance, if a trader aims to go long with 10x leverage and the market price of $ETH is 1000 $USDC, they can borrow liquidity from ranges centered at different prices, such as 900 $USDC and 950 $USDC, in the appropriate proportions. This allows traders to optimize their positions for their specific trading strategies.
• The InfinityPools matching engine abstracts the complexities of combining liquidity ranges and calculating interest rates from the trader’s perspective. When a trader places an order with a certain leverage multiple, the matching engine efficiently searches for and combines suitable liquidity ranges to offer the best possible interest rates. This user-friendly approach is reminiscent of Uniswap’s router, but tailored to optimizing interest rates within the InfinityPools ecosystem.

Benefits of the Matching Engine

The introduction of the matching engine brings several benefits to traders and liquidity providers within InfinityPools:

• Elimination of Liquidity Fragmentation: The matching engine mitigates liquidity fragmentation concerns by seamlessly combining liquidity ranges to provide comprehensive access to liquidity at various levels of leverage.
• Optimized Interest Rates: Traders benefit from the matching engine’s ability to search and combine liquidity ranges to obtain the most favorable interest rates for their trades.
• Customizable Leverage: Traders can easily achieve their desired leverage by borrowing from different liquidity ranges, and tailoring their positions to their specific trading strategies.
• Simplified User Experience: The matching engine abstracts technical complexities, offering traders a straightforward way to interact with the protocol and access the benefits of liquidity provision and trading.

Why the Project was Created

The development of InfinityPools protocol is driven by the need for genuine innovation in the DeFi space, addressing the limitations and shortcomings of existing offerings. Despite the initial promise of Layer 2 scaling solutions, many new products and protocols failed to deliver substantial value or improvements over established solutions. This phenomenon, known as the cycle of pseudo-innovation, highlights the importance of critically evaluating new protocols and primitives.

For instance, in order to reduce liquidation risk, futures exchanges limit the leverage available, the assets that can be traded, and the position sizes that can be achieved. Additionally, they often enforce liquidation penalties that can range from 1-3% of the positional notional and eat into the expected returns of traders. 

Options exchanges do not solve this suboptimal trading experience either. They often fragment liquidity even further across strikes and expiries, which also limits the potential for traders’ profitability and leads to a worse UX, making it hard to compete against centralized providers. 

Nonetheless, leverage is a highly in-demand instrument. Investing is only worth a person’s time if the return upside is high enough. 

The motivation for Infinity Pools also stems from the need to address the broken aspects of the DeFi landscape and unlock the true potential of decentralized finance. DeFi, while disruptive, has faced challenges that hinder its progress toward becoming a more open, efficient, and decentralized alternative to traditional financial systems.

One of the key issues in DeFi is the heavy reliance on external oracles, which introduce counterparty risk and limit the scope of improvements compared to Web2 or TradFi. Many protocols rely on oracles for price information, creating vulnerabilities related to timing, liquidity conditions, and external dependencies. Moreover, middlemen, such as liquidators or aggregators, add costs in the form of spreads and fees, reducing profitability for traders and liquidity providers.

To overcome these challenges, Infinity Pools adopts a first principles approach by reimagining primitives with zero external dependencies. By simplifying protocols to their fundamental components, Infinity Pools reduces attack surfaces and mitigates risks associated with external dependencies. This approach aligns with the concept of building on first principles, focusing on establishing a strong and simplified foundation that outperforms Web2 and traditional finance counterparts.

Sector Outlook

Leverage in traditional trading often involves borrowing funds to purchase more of an asset than could be acquired with the available margin. However, this approach comes with inherent limitations, especially when the asset’s price starts to decline. The competitive usage of spot liquidity can make it uncertain whether the asset position can be sold at a high enough price to cover the loan repayment. This problem intensifies with higher leverage ratios, where even a small downward price movement can lead to default. Derivatives like perpetual futures replicate similar constraints.

By addressing the challenges of traditional leverage mechanisms, InfinityPools introduces an innovative approach that revolutionizes the concept of leveraging assets. InfinityPools reimagines the process of creating leverage by pre-allocating the required spot liquidity to unwind the leverage position. This approach entails borrowing a concentrated Automated Market Maker (AMM) liquidity range from a public pool and placing it in a “private pool” accessible only to the trader. This secured liquidity range ensures that the leveraged asset position can be sold for the precise amount of borrowed cash, regardless of market fluctuations.

One of the most significant breakthroughs offered by InfinityPools is the elimination of liquidation risks in response to falling spot prices. The liquidity held within the “private pool” throughout the loan’s duration enables traders to sell their asset positions within the pool, mitigating the need for liquidation mechanisms. Furthermore, traders have the flexibility to choose where to execute their asset-to-cash swaps, whether within their “private pool” or on other decentralized exchanges offering better prices. This eliminates the reliance on external price oracles, liquidation bots, and other intermediaries, rendering the protocol completely autonomous and permissionless.

Potential Adoption

Perpetual futures are one of the few derivatives instruments that have found product-market fit in the dynamic landscape of crypto. As a derivative, perpetual futures enable traders to speculate on the price of assets over time, without the constraints of settlement or expiration. While this innovation has been well-received, Infinity Pools is taking it to an unprecedented level by addressing limitations that have impeded the evolution of perpetual futures trading.

Infinity Pools also enables the creation of structured products on any asset, eliminating bureaucratic hurdles and offering flexibility for developers to innovate. Traders and liquidity providers benefit from higher capital efficiency as well, as 100% of assets can be deployed. 

Structured products built on top of Infinity Pools also benefit from flexible withdrawals. Users can choose to withdraw immediately and pay a fee or withdraw gradually over time.

Securing Spot Liquidity: The Cornerstone of Unlimited Leverage in Infinity Pools

In the realm of trading, especially in leveraged trading, one of the major challenges is managing margin efficiently. In conventional systems, if an asset’s price starts to fall, there is no assurance that the position can be sold at a sufficiently high price to repay the loan acquired through margin. The problem intensifies as the leverage ratio increases because a higher leverage ratio means a smaller amount of margin, which in turn results in smaller price movements placing the loan at risk of default. In such systems, this limits the practicality of high leverage ratios, as the threshold for the downward price move that risks default can be impractically small. This is one of the reasons why most exchanges heavily rely on insurance pools to cover shortfall events.

Insurance funds are not necessary in Infinity Pools. The protocol addresses these limitations by securing spot liquidity in advance, which is essential for unwinding the leverage without incurring losses or defaults. In Infinity Pools, leverage is created through a loan of concentrated Automated Market Maker (AMM) liquidity. Essentially, the trader borrows a liquidity range from a public pool and places it into their private pool, which only they have access to for executing swaps.

By borrowing a liquidity range, the trader essentially secures the spot liquidity required to unwind the leverage position. This ensures that the asset position can be sold for the exact amount of borrowed cash, regardless of market movements. This is because a liquidity range inherently has reserves backing it. Hence, borrowing liquidity is synonymous with borrowing the cash necessary to purchase the leveraged asset holdings.

With this system, Infinity Pools essentially decouples the leverage ratio from the conventional limitations arising from spot liquidity competition. By securing the necessary spot liquidity beforehand, the system allows for significantly higher leverage ratios without the associated risks of liquidation or default that are prevalent in traditional systems.

Eliminating Liquidations and Oracles

One of the pioneering features of Infinity Pools is the elimination of liquidations even when the spot price of an asset declines. Since traders borrow liquidity from a public pool and place it into their private pool, this private pool holds the liquidity for the duration of the loan. 

The importance of this is that the asset position can be sold in the private pool just before repaying the loan, irrespective of how low the spot price has fallen in the market. Essentially, the private pool acts as a secured reserve that ensures the trader can always execute swaps for repaying the loan, eliminating the need for liquidation processes that are common in other platforms. This is also extremely beneficial for traders since they will avoid the liquidation penalties that they would incur if they were using any other platform. There are no liquidation penalties in Infinity Pools, which increases the expected returns for traders.

Chains

InfinityPools uses Ethereum as its settlement layer.

Using the Protocol

Where standard perpetual futures platforms impose limitations in leverage, and asset listings, and are susceptible to liquidation risks and dependence on oracles, Infinity Pools makes a paradigm shift.

There are two sides: liquidity providers and traders.

• Liquidity providers either deposit assets directly into the protocol, or lend their Uniswap v3 LP positions to the protocol.
• Traders borrow LP positions and swap the reserves backing the LP token for the asset they want to long. This is similar to how margin trading works, where the funds are borrowed from a broker and swapped to achieve the desired position.

Let’s work with the example where the current market price of $ETH is $2,000.

Assume a liquidity provider lends out an ETH/USDC LP token on InfinityPools. The LP token is worth 2,400 $USDC and is deployed in a tight liquidity range centered at 2,200 $USDC.

A trader looking to go long on Ethereum with leverage decides to borrow this LP token and redeem it for 2,400 $USDC. With the current market price of Ethereum at 2,000 $USDC, the trader swaps the 2,400 USDC for 1.2 $ETH (minus fees and slippage) on a spot DEX (using 1inch in the backend).

Here, we consider three possible scenarios:

• A) If the price of $ETH rises, the trader makes a profit. They can swap a part of the 1.2 $ETH back to 2,400 $USDC to repay the LP token.
• B) If the price of $ETH decreases to just above 2,200 $USDC, the 1.2 $ETH the trader holds is worth around 2,640 $USDC, and the liquidity provider is expecting back an LP token worth 2,400 $USDC. The trader can still repay the LP token, and the initial collateral requirement would be lower in this case.
• C) If the price of $ETH drops below 2,200 $USDC, the liquidity provider is expecting back an LP token worth an amount close to 2,400 $USDC. The trader holds 1.2 $ETH and would need to ensure that they have enough collateral to repay the full LP token, which would require additional collateral to cover the difference.

In this specific example, the minimum collateral requirement for a trader borrowing an LP token worth 2,400 $USDC at the 2,200 $USDC liquidity range would depend on how close the borrowed liquidity range is to the current market price of $ETH. The closer the liquidity range to the current market price, the more leverage it enables. For example, if the liquidity range borrowed was deployed at $1,999 $USDC, the maximum loss / initial collateral required would be 1 $USDC, which corresponds to 1,000x leverage.

Liquidity Providers

Liquidity providers play a vital role in the InfinityPools ecosystem, benefiting from unique mechanisms that offer potentially higher yields compared to spot AMMs. 

Yield Comparison with Spot AMMs

Liquidity providers are incentivized with a continuous and higher yield than what they would be earning in the underlying Uniswap pools. Even when their liquidity is out of range, they will continue accruing yield by virtue of being lent out to borrowers who pay interest.

 This advantage stems from the utilization of liquidity for both spot trading flow and as collateral for leverage, increasing the overall utilization of the provided liquidity.

Aligning Yields with Options Premiums

Liquidity providers can gauge the fairness of their compensation by considering whether they are pricing volatility appropriately. To achieve fairness, InfinityPools employs a dual-component interest payment structure: the floor rate and the utilization rate.

• The floor rate, calculated based on an equation akin to the Black Scholes model, aims to compensate LPs at implied volatility levels. 
• The utilization rate, responsive to market supply and demand, can drive LP yields above implied volatility levels. 

This alignment ensures that liquidity providers are compensated fairly, in line with options premiums.

Liquidity Withdrawals

Liquidity providers have flexibility in withdrawing their assets from InfinityPools. 

When it comes to withdrawals, liquidity providers have two options:

• Withdraw immediately (for a fee) – If the utilization rate is below 100%, immediate withdrawal is possible for a fee. This fee covers the cost of borrowing the liquidity provider’s assets that are still in use.
• Withdraw gradually (for free) –  If the utilization rate is, for instance, 20%, liquidity providers can instantly withdraw 80% of their assets. The remaining assets follow an exponential unlocking schedule, with 50% accessible after 1 day, 75% after 2 days, and so forth.

Benefits of Liquidity Provisioning

InfinityPools’ liquidity provisioning offers several advantages for participants:

• Out of Range Yields: Liquidity providers earn yield even when their liquidity is not within the specified range. This feature enhances the attractiveness of participating in the protocol.
• Resistance to Just-in-Time (JIT) Strategies: The protocol’s design discourages strategies where liquidity is deposited briefly to claim disproportionate fees generated. This approach promotes a fair and sustainable ecosystem for liquidity providers.

Traders

The main advantage for traders is that they can post a predetermined amount of collateral and stay away from the risk of default. In return, they will pay ongoing interest to keep their loan positions open and repay their loans in either of the base assets that make up the LP. 

Leverage Calculation and Availability

Traders’ leverage is determined by the ratio of their position size to the initial collateral deposited. The initial collateral consists of both the margin required to cover potential losses and the initial interest rate payment. However, leverage availability varies based on asset pairs’ volatility and liquidity. 

• More volatile pairs result in lower leverage.
• More stable pairs offer higher leverage. 
• Liquidity in InfinityPools can also impact the achievable leverage.

Position Duration and Interest Payment

While InfinityPools eliminates the risk of liquidation, traders can’t maintain positions indefinitely. Positions remain open as long as traders pay the interest for their leverage. 

The protocol utilizes deposited collateral and unrealized profits to cover the interest rate. 

• Successful trades can be extended indefinitely by reinvesting unrealized profits. 
• If a position exhausts its collateral and profits to cover interest, and the trader doesn’t close it, the position will start unwinding exponentially.

Entries and Exits

InfinityPools traders benefit from favorable entry and exit fees by utilizing the entire spot market. Trades can be executed using any spot DEX or DEX aggregator. The platform’s UI incorporates a DEX aggregator (currently 1inch) for order execution. For leveraged spot trades, slippage on entry works in favor of the trader’s exposure, and exit can be executed through a TWAP, minimizing slippage impact.

Interest Rates and Options Premiums

Interest rates on InfinityPools may differ from options premiums. Traders can arbitrage the rates to align them more closely. 

For instance, 

• If InfinityPools rates are below options premiums, traders can use a strangle strategy to buy up cheap volatility, pushing InfinityPools rates higher.
• Conversely, if rates are above options premiums, traders can provide liquidity to the protocol and hedge their exposure with options.

Arbitrageurs

When funding is too cheap (implied volatility too low), arbitrageurs can borrow liquidity (which pushes up funding), go long and short simultaneously (aka. strangle), and exit once the price moves into profit. This is analogous to betting on volatility with a long strangle position. 

In other words, arbitrageurs come in when funding is perceived to be lower than the chance of an X% price move, creating room for profit. This way, LPs are always paid at least the realized volatility rate.

Additional Use Cases

Infinite Structured Products

Infinity Pools allows liquidity providers to structure their liquidity positions to emulate traditional financial instruments such as covered calls or cash-secured puts. These structured products offer several advantages:

• Any Asset: They can be created for any asset, even those lacking perpetual, options, or spot markets.
• Any Payoff: The structure permits permissionless creation with flexible payoff structures, alongside the ability to withdraw capital at any time exponentially.
• No Fees: There are no fees payable to market makers for rolling over positions, reducing the cost burden on liquidity providers.

More Powerful Flash Loans

Infinity Pools enhances the concept of flash loans, typically used for immediate and short-lived arbitrage opportunities within a single transaction. The platform’s “Swappers” provide:

• More Time: Unlike traditional flash loans that must be settled in a single transaction, Swappers can offer up to 1000x leverage over multiple blockchain blocks.
• Returned Tokens: Swappers allow for the return of any combination of the pool’s two tokens, as long as they adhere to the proportions dictated by the strike price.

Multi-Block Arbitrage

Infinity Pools supports complex arbitrage strategies across DEXs that span multiple blocks, allowing:

• Extended Timeframe: Arbitrageurs can borrow significant amounts of assets for several blocks, enabling them to execute trades that are temporally separated—similar to traditional cross-exchange arbitrage.
• Reduced Miner Extractable Value (MEV): These multi-block strategies are less susceptible to being front-run by miners, thus significantly reducing the risk of MEV.

Example Arbitrage Strategy:

1. Borrow $ETH at a strike price close to the current market price.
2. Swap $ETH for $USDC on DEX A.
3. At a later time, swap $USDC back to $ETH on DEX B (potentially the same as DEX A but at a more favorable rate).
4. Return the borrowed $ETH to complete the trade.

Business Model and Revenue Streams

• Interest Rate Spread: InfinityPools offers loans to traders by enabling them to borrow liquidity ranges and utilize them for leveraged trading. The interest rate paid by borrowers includes two components: the fair value interest rate (floor rate) and a utilization rate. The utilization rate allows the platform to generate revenue by lending out liquidity ranges at rates higher than the floor rate. This interest rate spread between what borrowers pay and what liquidity providers receive forms a significant part of InfinityPools’ revenue.
• Platform Fees: InfinityPools charges fees to borrowers for utilizing the platform’s lending services. These fees contribute to the platform’s revenue stream. 
• Matching Engine Efficiency: The platform’s off-chain matching engine pairs traders and liquidity providers in a way that minimizes liquidity fragmentation, optimizes interest rates, and ensures efficient trades. InfinityPools may charge a nominal fee for facilitating these matched trades, enhancing the user experience while generating revenue.
• Strategic Partnerships: InfinityPools can explore collaborations and partnerships with other DeFi projects, protocols, or platforms. These partnerships can introduce new users to the platform, create cross-promotional opportunities, and potentially lead to revenue-sharing arrangements.

Risks

In addition to smart contract risk from vulnerabilities and coding errors, Infinity Pools is exposed to market risk that stems from price volatility and active portfolio management by traders and liquidity providers. However, what stands out is the ability to overcome both credit and counterparty risk. 

Zero Credit Risk

One of the key features of Swappers within Infinity Pools is that they are positions that are always fully collateralized by their reserves. This means that at any given time or price, the value of the reserves backing a Swapper is equal to or greater than the value of the borrowed liquidity. This feature is critical in ensuring that there is no credit risk associated with the Swapper; credit risk being the risk that a borrower will default on any type of debt by failing to make required payments.

In traditional leveraged trading, if the value of a trader’s position falls below a certain threshold, they face liquidation where the position is forcibly closed to prevent further losses. In the context of Infinity Pools, instead of facing liquidation, the reserves can be swapped through any cryptocurrency aggregator or decentralized exchange (such as 1inch) to adjust the ratios of token1/token0. Essentially, this means that the position can be rebalanced rather than liquidated.

This benefits both liquidity providers and traders and creates a positive feedback loop where better LP yields attract more liquidity providers, leading to deeper liquidity conditions which enable better trade execution with low slippage.

• LPs earn premiums for lending out their liquidity pool tokens. This acts as an additional source of income alongside the traditional trading fees, making it more profitable to be a Liquidity Provider.
• The increased profitability for LPs translates to deeper liquidity in Infinity Pools. Deeper liquidity, in turn, results in better trade execution. This is because, with more assets in the liquidity pool, trades have less impact on the price, leading to lower slippage.

Counterparty Risk

Counterparty risk refers to the possibility that the other party in a transaction may not fulfill their contractual obligations. InfinityPools mitigates this risk by eliminating liquidations, relying on mathematical settlement, being oracle-less, and maintaining a non-custodial nature. 

However, traders should always be cautious of smart contract risks and conduct their own research. While the protocol undergoes rigorous security measures, users must remain mindful of potential exploits.

Liquidity Risk

Unlike platforms like Uniswap, which evolved through iterative versions and had substantial TVL to support liquidity transitions, Infinity Pools lacks a foundational liquidity base (such as a previous version’s TVL). This absence could impede its ability to quickly establish a robust liquidity pool, essential for its concentrated liquidity AMM model.

Security

The protocol is undergoing audits by third-party firms before the mainnent launch.

Project Investors

The Lemma Labs team is the main source of contributions for the InfinityPools protocol. They hold degrees from Cambridge University, Princeton, Columbia, and other universities, and their previous companies include 0x, Goldman Sachs, Bridgewater, Uber, Google, Facebook, and Microsoft.

Lemma Labs completed a seed round in December 2021 with the following investors:

FAQ

Liquidity Providers FAQ

Is the yield on InfinityPools going to be higher than spot AMMs?

While no guarantees can be made due to various factors, the InfinityPools LP yields are designed to be potentially higher on average than those of traditional spot AMMs. The utilization of liquidity for both spot trading flow and collateral for leverage contributes to this potential yield advantage.

What does it mean for LP yields to be in line with options premiums?

This metric means that liquidity providers are compensated fairly for selling volatility. InfinityPools achieves this through a dual-component interest payment structure: the floor rate, determined by an equation similar to the Black Scholes model, compensates at implied volatility levels. The utilization rate, responsive to supply and demand, can elevate LP yields to align with options premiums.

Can liquidity providers withdraw their liquidity immediately?

Yes, unless the utilization rate is at 100%, liquidity providers can withdraw their liquidity instantly for a fee. This fee covers the cost of borrowing the assets still in use. For free withdrawals, conditions apply. For example, if the utilization rate is 20%, liquidity providers can withdraw 80% of their assets instantly, with the remaining portion unlocking on an exponential schedule.

What are the advantages of liquidity provisioning on InfinityPools?

Liquidity provisioning on InfinityPools comes with various advantages, including earning yield even when liquidity is not within the specified range, discouraging just-in-time strategies, and benefiting from the potential for higher yields compared to spot AMMs.

Traders FAQ

Can traders get 10,000x leverage on all assets?

Unfortunately not. Leverage is calculated based on the position size and initial collateral deposited. The initial collateral includes both the margin to cover potential losses and the initial interest rate payment. Higher volatility assets will have higher interest rate payments, leading to varying levels of leverage availability. Liquidity in InfinityPools can also potentially limit leverage.

If traders can’t get liquidated, does that mean they can keep a position open forever?

No, traders can only keep a position open as long as they continue to pay the interest for their leverage. InfinityPools uses deposited collateral and/or unrealized profits to cover the interest rate. Trades have a base time limit, extendable by using unrealized profits. If a position runs out of collateral and unrealized profits to pay interest, and it’s not closed by the trader, it will start unwinding exponentially.

What are the fees to enter and exit positions?

InfinityPools traders achieve optimal prices by executing orders in the entire spot market. The platform allows entering and exiting trades using any spot DEX or DEX aggregator. The InfinityPools UI employs a DEX aggregator like 1inch to execute orders. Leveraged spot trades (offered by InfinityPools) experience slippage on entry that favors the trader’s exposure and exit can be executed through a TWAP to mitigate slippage.

Will the interest rates always be in line with options premiums?

No, interest rates and options premiums may differ at times. Traders can arbitrage these rates to bring them closer together. If InfinityPools rates are below options premiums, traders can create a strangle to buy up cheap volatility, pushing InfinityPools rates higher. If InfinityPools rates exceed options premiums, traders can provide liquidity to the protocol and hedge exposure with options.

What is counterparty risk and what are some other risks to be mindful of?

Counterparty risk refers to the possibility of the other party not fulfilling its contractual obligations in an investment or trading transaction. InfinityPools mitigates counterparty risk through its design – no liquidations, reliance on oracles, or custody of assets. However, users must remain aware of smart contract risks and do their research, as vulnerabilities could lead to fund loss. The protocol has undergone audits to enhance security, but due diligence is essential.

Community Links

• Website
• Docs
• Twitter
• Medium
• Discord